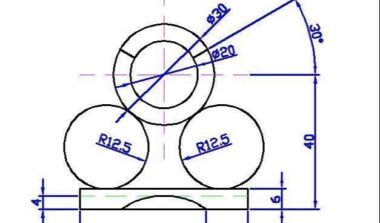
CAD三点画圆的逆用,先看看原题目吧。
首先分析此图:
如果给上图添加一条直线,然后 将此图分为上下两部分,你会发现什么?
由于,上下两部分各有一个直角,那么,根据直角三角形的特殊性,可以知道,上下两部分中,点A、B、E 落在同一个圆上,点B、E、C落在另一个圆上。
然后根据圆中同一条弦所对应的圆周角等于圆心角的一半这个定律的逆用,可以知道:其实两个圆是一样的,也就是说图中的四个点A、B、C、E是落在同一个圆上的,并且BE的长即为圆的直径。
再根据,在同一个圆中,如果弦相等,那么弦所对应的圆周角也相等。在这个图中,也就是说由于BC=EC,那么∠CAB=∠CBE=45°。
知道了这些,这个题就很容易解决了。
1、 画水平直线,长度为80。
2、将水平直线旋转45°,或者相对坐标法得到。
3、将通过A、B、C三点画圆。
4、过A两向上做构竖直线,交圆与点E。
5、 连接EC,BC成线即可。
6、修剪操作,清理图形。
7、标注检验正误。
8、检验EC和BC的长是否相等,得到C的数值。
9、再次标注,得到a、b的长度。
总结:本题的难点在于找到入手点,先分析图形,利用数学的几何原理来发现隐藏的条件时解题的重点。