有限元网格是有限元走向工程应用的桥梁，在有限元分析中占有重要的地位。有限元网格的生成是指将连续的几何模型离散成为计算所需的单元信息，其质量的优劣直接影响求解的速度与精度。本文中小编将简要为大家介绍几种常用的有限元网格生成方法。
映射法是最早出现且最直观的一种有限元网格生成方法。在有限元网格发展早期，常采用扫掠法和拖拽法对简单四边界区域进行网格生成。将已剖分的起始边上各点沿特定的方向移动若干次至终止边，即完成对区域的剖分。此类方法实际上就是一种映射，采用向量作为坐标变换方式。
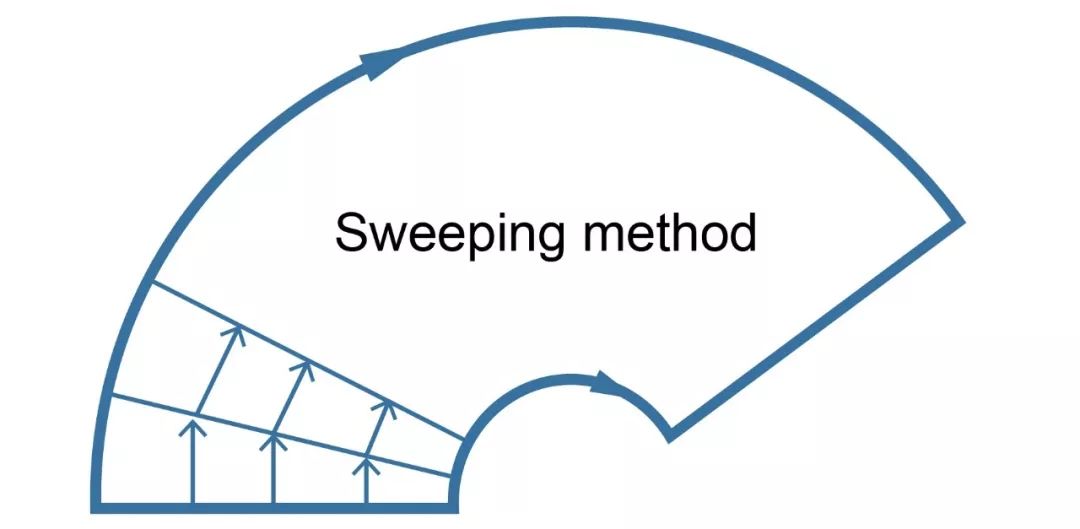【 扫掠法 】
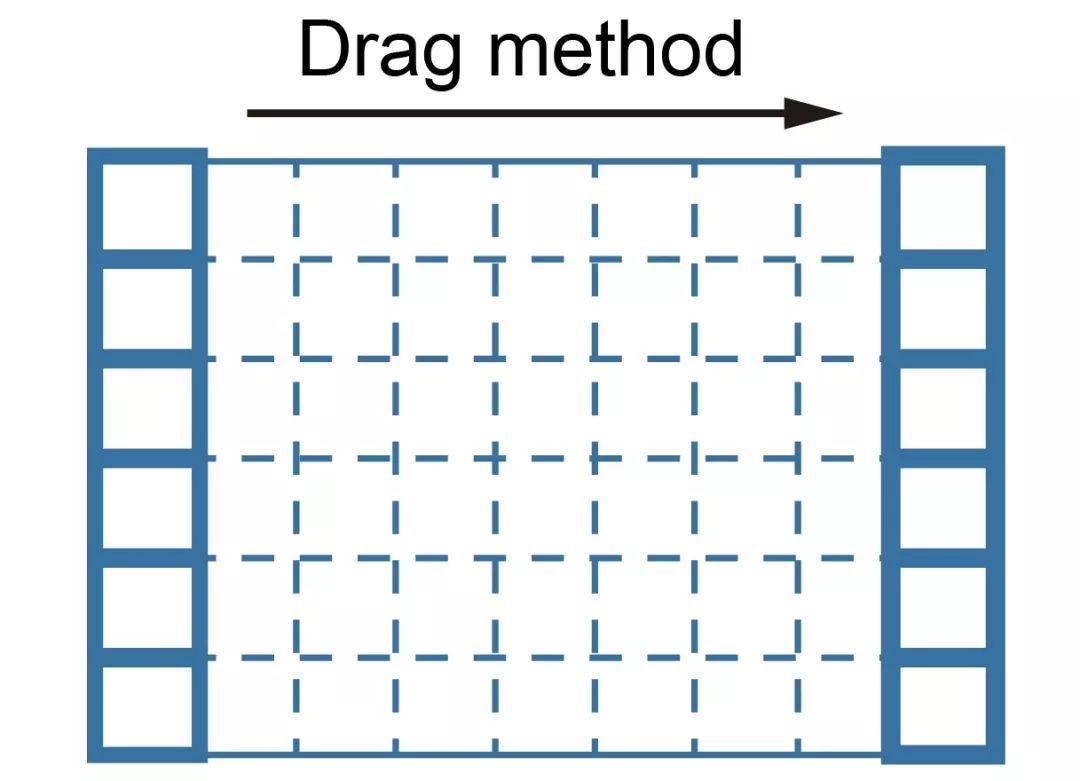
【 拖拽法 】
映射法的核心在于坐标变换，其基本步骤如下：
-
通过适当的映射函数将待剖分物理域映射到参数空间中形成规则参数域；
-
对规则参数域进行网格剖分；
-
将参数域的网格反向映射回物理空间，从而得到物理域的网格。
映射函数有很多种，可根据实际问题进行选取。若区域的四条边都为直线，可以采用四节点四边形的拉格朗日插值函数进行坐标变换；若区域的边界为曲线，则可以将边界表示为参数形式C=C(t)，同样可以将待剖分物理域映射至单位正方形参数域。此外，还可以采用偏微分方程法，通过数值求解偏微分方程而得到参数空间与物理空间之间的映射关系。
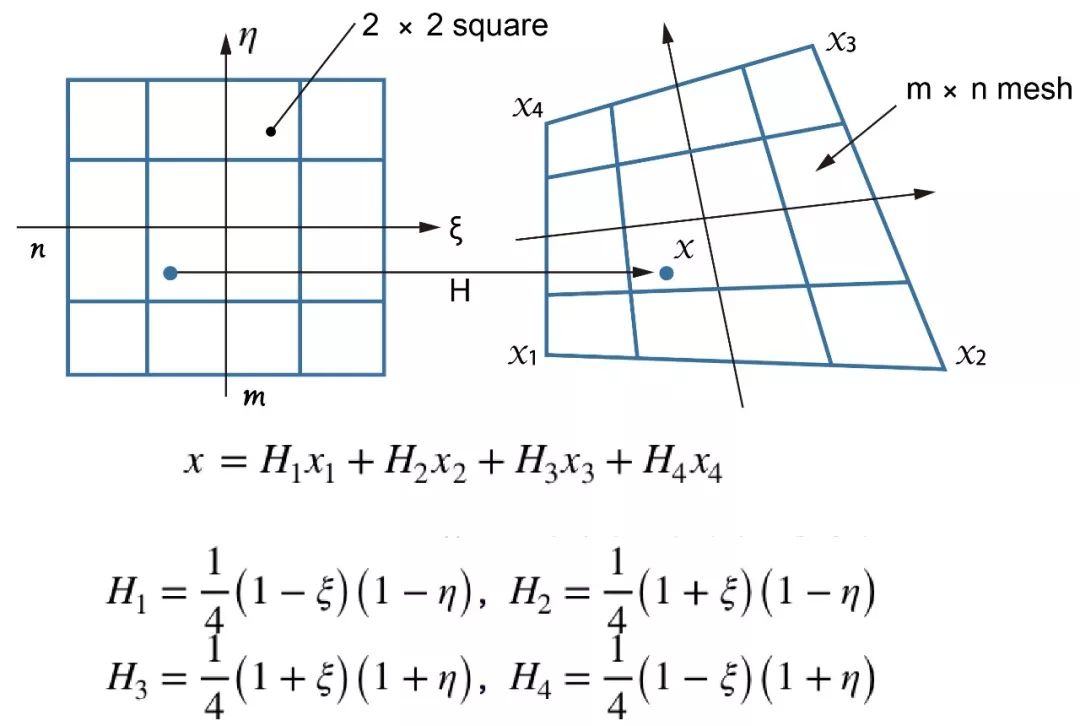
【 拉格朗日插值函数 】
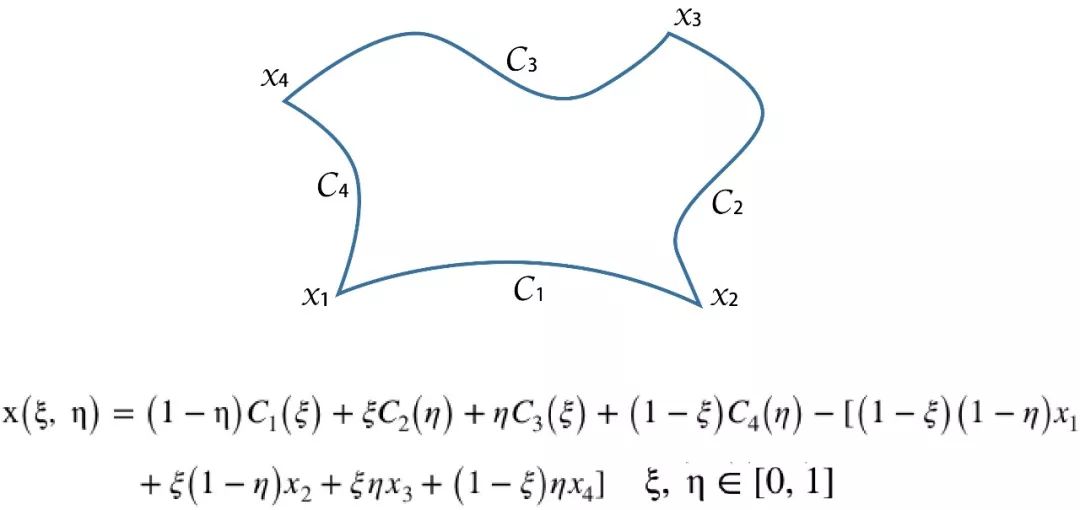
【 将边界表示为参数形式C=C(t) 】
映射法更大的优点在于既能生成结构化网格，也能生成非结构化网格。映射法对单连通区域算法简单、速度快、单元质量好，并且适用于曲面网格生成，可与形状优化算法集成。因此，映射法在众多的商业有限元分析软件中占有重要的地位。
然而，映射法在实际应用中也存在许多难点，首先便是如何将复杂的多连通区域分解为若干可映射的子区域。目前在实际应用中，采用映射法处理复杂几何体的时间往往远大于网格生成的时间。此外，处理子区域之间网格的协调性和指定区域网格的疏密过渡问题，对用户有着较高的要求。
四（八）叉树法是一种基于栅格法的全自动非结构化网格生成方法。栅格法的特点是用一组背景栅格覆盖剖分区域，删除区域之外的栅格，并以剩余部分作为初始条件生成网格。Yerry和Shephard首先将用于近似表达几何对象的四（八）叉树空间分解法引入到网格剖分领域，利用四（八）叉树数据结构，可对背景栅格递归细分，逼近边界。
以二维为例，四叉树法的基本步骤如下：
-
将剖分区域的边界离散化，得到一组线段集和点集；
-
创建背景栅格覆盖目标区域，根据点集的分布平衡四叉树；
-
保留与目标区域相交的栅格，删除完全落在目标区域之外的栅格；
-
内部栅格与边界栅格的相容网格剖分；
-
网格优化。
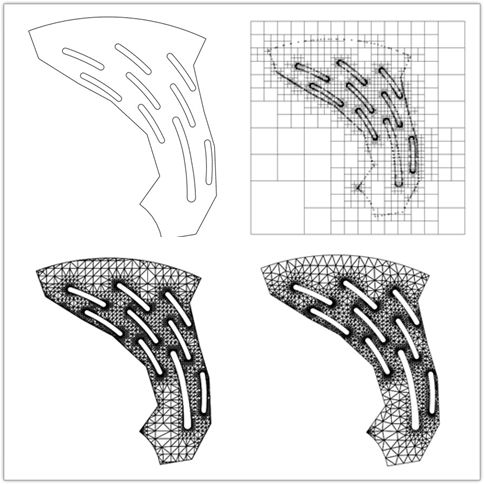
【 四叉树法 】
四（八）叉树法的难点在于内部栅格与边界栅格的相容网格剖分。以四叉树为例，在平衡叉树的步骤中，通常会将相邻区域之间的细分等级之差限制在1以下，使每个区域仅会在顶点和边中点处产生网格点，以减少相容网格剖分时所需的模板数量。然而，对于三维八叉树而言，即使相邻区域之间细分等级之差不大于1，也需要建立至少78种模板。为此，有许多学者致力于降低八叉树法程序实现的复杂度。
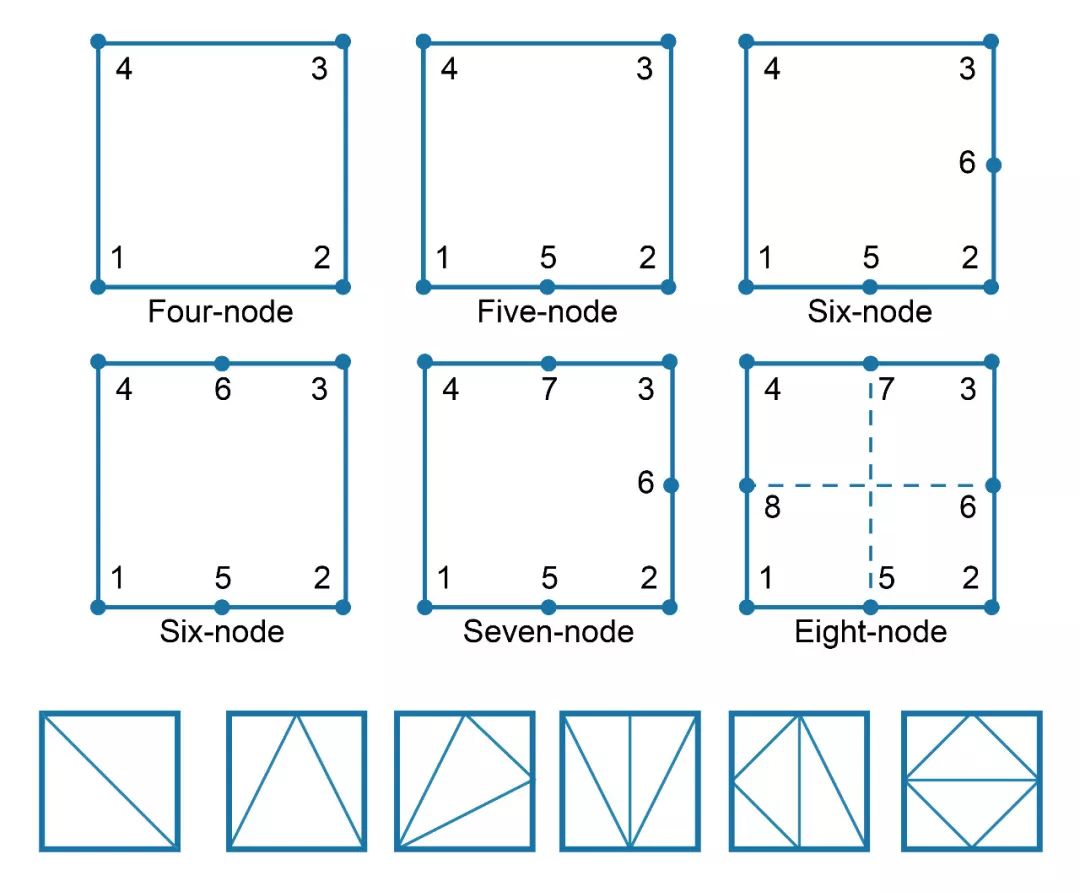【四叉树相容剖分模板 】
[1] S.H. Lo, Finite Element Mesh Generation, CRC PressTaylor & Francis USA, 2015
[2] PJ Frey, L Marechal, Fast Adaptive Quadtree MeshGeneration, 7th International Meshing Roundtable, 1998
由于篇幅有限，今天只为大家介绍映射法(Mapping)和四（八）叉树法 (Quadtree/Octree)两种有限元网格生成方法。