利用 Simcenter MAGNET™ v7.9 软件中的磁滞模型，工程师和科学家们可以将铁损效应融入低频电磁装置的仿真中，从而对真实场景建模。通过完整的磁滞回线而不是   SV（单值）磁化曲线来精确表示铁磁材料，会影响局部结果量， 如磁场分布。其结果是，装置的工作点和其他全局量（如输入功率、扭矩／ 力等）也会改变，这对于装置的多目标优化以找到更佳设计可能很关键。在Simcenter© 环境中对电磁装置进行多物理场仿真时，磁滞模型的融入对于这些材料的精确建模也是至关重要的一步，这些材料的磁特性也会受到机械应 力和高温的影响。

有限元 (FE) 方法广泛用于商业计算机辅助设计 (CAD) 软件行业，用以分析和设计低频电磁装置，例如执行器、电机和变压器。麦克斯韦方程组被离散化以计算复杂几何形状的磁场，否则无法进行仿真。人们已开发出先进的数值技术来提高求解结果的精度，以便更好地预测这些电磁装置的性能。然而，如果制造这些装置的铁磁材料的磁特性未在 CAD 仿真中得到正确建模，场结果将是不准确的。

在商业软件中，铁磁材料的磁特性通常用非线性单值(SV) 磁化曲线（称为磁化曲线，示例如图 1 所示）来建模，其原因有多方面，包括数值稳定性、可用计算资源有限、缺乏材料数据等。这种近似得到的是无磁损仿真， 意味着全局结果（例如电机转矩）不包括任何磁（铁） 损。然后在后处理阶段进行计算，采用的通常是 20 世纪

早期开发的经验损耗公式。以下等式 (1) 表示这种场景中的能量平衡。

(1) Einput = Eoutput + Eohmic + EStoredMag

(1) 中的 Eohmic 和 EStoredMag 项分别是欧姆(I2R) 损耗和材料中储存的磁能。注意，(1) 中没有铁损项，这意味着 SV 仿真没有在场结果中包含铁损。

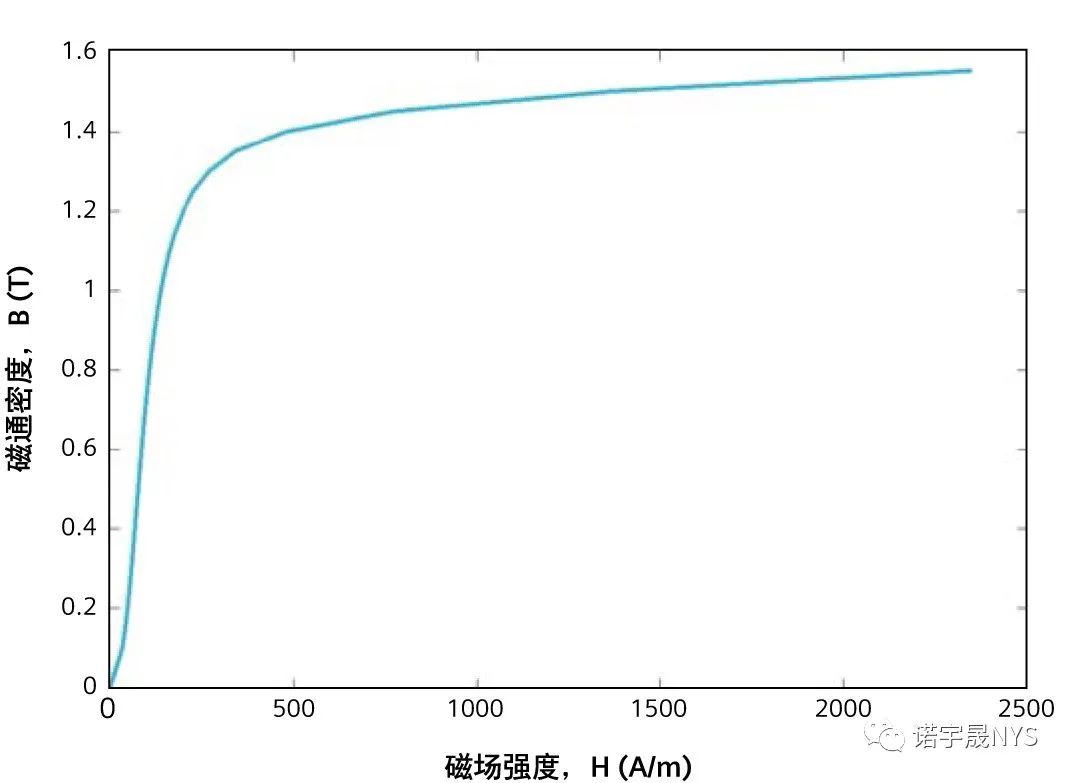
图 1：35WW300 无取向电工钢的单值 磁化曲线。

实际上，铁磁材料表现出来的不是 SV 磁化曲线，而是磁滞回线（如图 2 所示）。当施加的磁场强度 H 改变时， 能量以热的形式在材料内部耗散。由此造成的损失称为磁滞损耗。在 FE 仿真中包含磁滞会修改能量平衡方程 (1)， 如下所示。

(2) Einput = Eoutput + Eohmic + Ehys

(2) 中的 Ehys 项表示铁磁材料中的磁滞损耗和储存的磁能。因此，对于磁滞仿真，Simcenter MAGNET v7.9 禁用了储存的磁能和磁共能选项卡。这将在下一节的单片测量仪 (SST) 示例中详细说明。

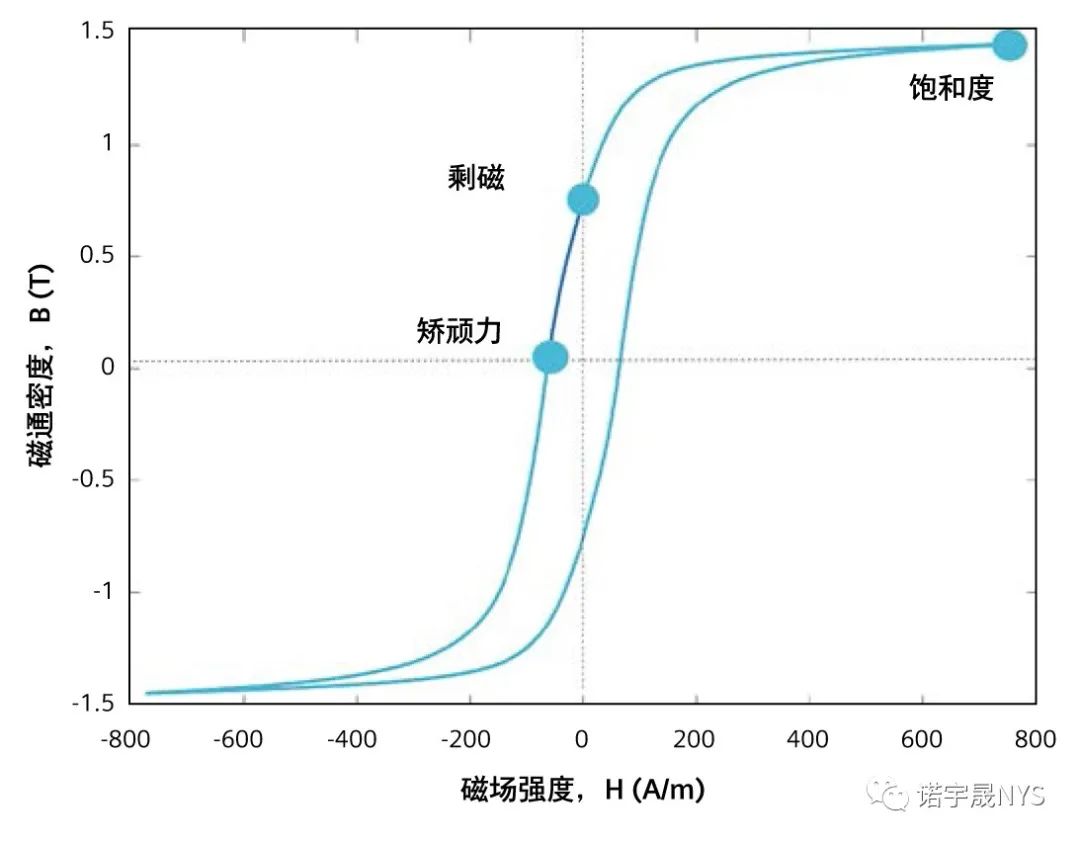
图 2：35WW300 无取向电工钢的磁滞回线。

尽管有强大的计算机和先进的数值技术，但商业软件中包含磁滞模型的仍然很罕见。虽然学术研究已经建立了许多磁滞模型，例如 Jiles-Atherton [1] 和 Preisach [2] 模型，但商业 FE 软件公司并没有普遍采用它们来精确表示现代电磁装置（如执行器、磁存储和记录装置、电力变压器、变速电机等）仿真中铁磁材料的磁行为。现今由于仿真时间已经缩短（源于处理器速度更快），可以在这些装置的复杂几何形状中大规模采用计算代价很高的磁滞模型。

Siemens 的 Simcenter MAGNET 是一款通用二维／三维电磁场仿真软件，适用于从简单到复杂的电磁和机电装置的虚拟原型设计。使用 Simcenter MAGNET，工程师和科学家们可以设计电机、传感器、变压器、执行器、电磁阀或任何带有永磁体或线圈的部件，节省时间和金钱。

本文重点介绍 Simcenter MAGNET v7.9 的一项新型高级功能的应用，该功能允许用户采用矢量 Jiles-Atherton 磁滞 (Hys) 模型 [3] 将磁滞纳入场结果中。当利用二维瞬态求解器（有和无运动）求解仿真时，可以启用该功能。

本节讨论纳入磁滞模型对局部磁场和铁损以及全局结果

（例如电流、电压、力／扭矩和各种电磁装置的瞬态现象）的影响。还会介绍其与常规 SV 模型的比较。

1. 单片测量仪 (SST) 

在实验室中测量钢的磁特性时使用钢带（尺寸：30mm ×250mm × 0.35mm）和磁测仪，例如单片测量仪 (SST)、Epstein 方圈等。第一个应用实例是单个 SST 样品本身。

SST 样品的 Simcenter MAGNET 模型如图 3(a) 所示。激励线圈环绕该样品，线圈中的电压可以调节，以便在样品中获得所需的磁通密度 B。

图 3：单条 35WW300 无取向电工钢带的仿真模型 (a) 实体视图，使用 (b)单值 (SV) 模型和 (c) 磁滞 (Hys) 模型计算的均匀 B 场，时间为 15 毫秒（正弦激励的峰值）。

针对 35WW300 无取向电工钢，使用 SV 和 Hys 两种模型求解该模型。t = 15 ms 时，使用两种模型的 B 场图如图 3 (b) 和 (c) 所示。对于 SV 模型，在后处理阶段中计算铁损时使用 Simcenter MAGNET 中的经验损耗公式，如下所示。

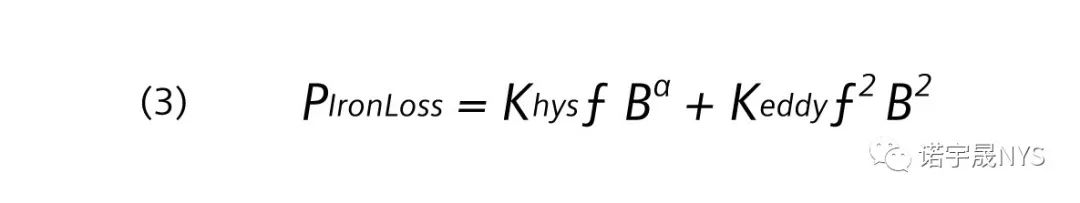
其中，Khys、α 和 Keddy 是利用用户提供的功率损耗曲线确定的材料损耗系数。使用 Hys 模型时，(3) 中的磁滞损耗项，即 KhysƒBα 被 (4) 替换，以计算磁滞回线的面积。

在 Bmax = 1.13T 时使用两种模型计算的样品线圈电流如图 4 (a) 所示。测量和计算的磁滞回线（使用 Hys 模型） 的比较显示在图 4 (b) 中以反映 Hys 模型的准确性。使用SV 和 Hys 模型，施加不同幅值的正弦电压来计算不同感应水平下的铁损，结果如图 5 所示。

图 4：(a) 使用 SV 和 Hys 模型在 Bmax = 1.13 T 时计算的线圈电流；(b) 在

Bmax = 1.13 T 时的计算和测量的 磁滞回线

图 5：测量和使用 SV 和 Hys 模型计算的铁损。频率为 50 Hz。

对于使用 SV 和 Hys 模型的 SST 样品，Simcenter MAGNET 计算的储存磁能如图 6 所示。如前所述，使用 Hys 模型的磁滞损耗计算还包括储存的磁能，其随时间累积。因此，对于 Hys 模型，Simcenter MAGNET v7.9 中的储存磁能被禁用。然而，当使用 SV 模型时，磁滞损耗不包含在场结果中，储存的磁能可以直接从 SV 曲线计算。

图 6：储存的磁能。对于 Hys 模型，它表示以磁滞损耗消耗的能量随着时间推移而不断增加。

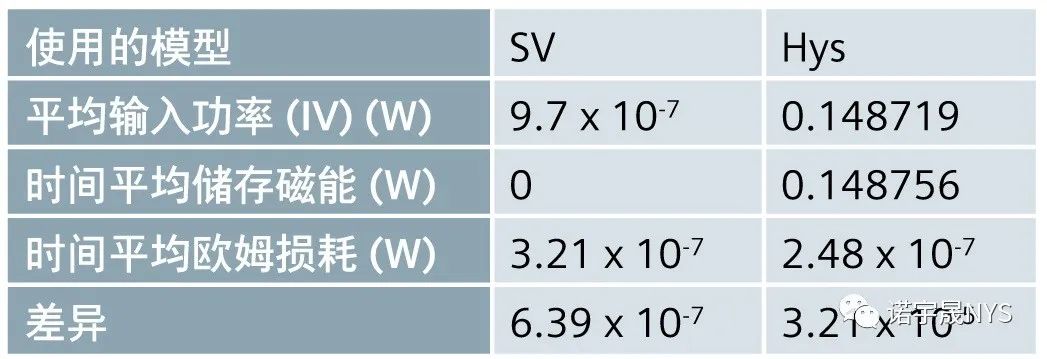
表 1 显示了对于一个完整的激励周期，使用两个模型的功率平衡。可以看到，对于 SV 模型，时间平均储存磁能为零。然而，时间平均储存磁能（磁滞损耗）是功率平衡方程的一部分。两种模型均有的微小差异是由数值积分误差造成的，可以忽略不计。

表 1 – 功率平衡（一个激励周期，频率 = 50 Hz）

2.Team 32 问题 

试验台是一个三柱式铁磁芯，如图 7 (a) 所示。铁磁芯由五层叠合而成，Fe-Si 含量为 3.2%，每层厚度为 0.48mm， 电导率 σ= 1.78 MS/m，质量密度 δ= 7650 kg/m3。两个 90 匝的绕组绕在外柱上，每个绕组的直流电阻为0.32 欧姆。这些绕组既可以串联连接，也可以由两个独立控制的电压源供电。

这里我们仅考虑两个绕组由两个独立的正弦波激励的情况，其幅值为 14.5 V，频率为 10 Hz，相位差 90o。这样， 装置的中心柱上部磁场可以旋转（图 7 (a) 中的 P 点处）。

该问题的 Simcenter MAGNET 模型如图 7 (b) 所示。使用SV 和 Hys 模型，运行仿真 125 毫秒（1.25 个激励周期， 每周期 40 个点）。使用两种模型在 t = 75ms 时计算的B 场的阴影图分别如图 8 (a) 和 (b) 所示。可以看到，对于 Hys 情况（如图 8 (b) 所示），最右柱中几乎不存在通量线，而且拐角处的通量线在自身闭合。B 场和 H 场的箭头图分别如图 9 和 10 所示，用以研究这种现象。可以看到，最右柱上的 H 场在 0 A/m（外拐角）到接近100 A/m（内拐角）之间变化。在图 9 (a) 和 10 (a) 所示的 SV 情况中，B 的符号随 H 变化，即 SV 磁化曲线通过原点（H = 0，B = 0）。但在 Hys 情况中，铁磁材料具有矫顽力，当 H 达到矫顽力时 B 反转，因此在同一拐角中，场节点的 B 符号不同，即 H 未改变符号，B 却改变符号。

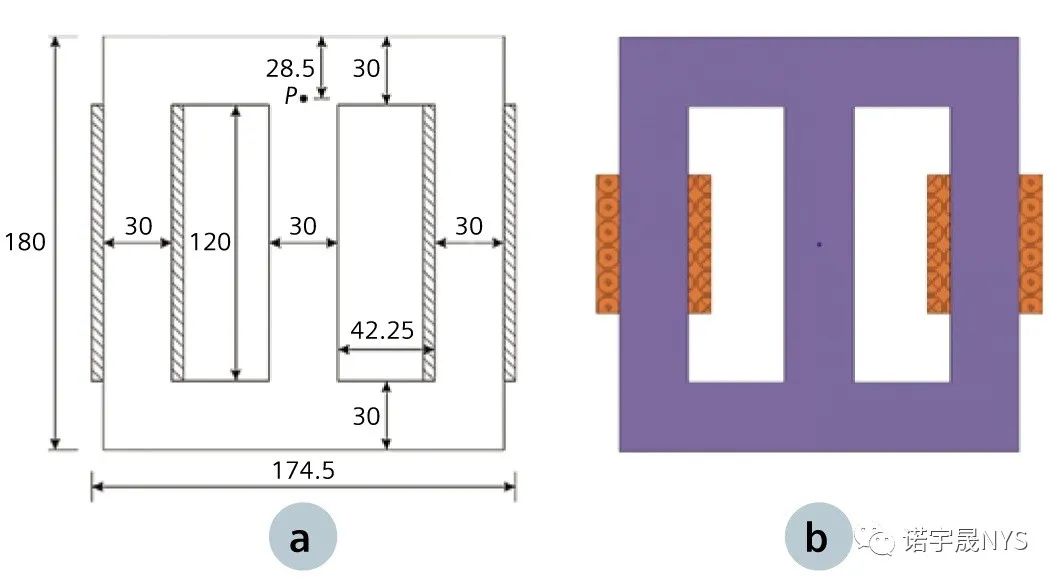
图 7：(a) 三柱式变压器的几何形状 [6]（尺寸单位为 mm）(b) SimcenterMAGNET 模型。

图 8：使用 (a) SV 和 (b) Hys 模型计算的在 t = 75 ms 时的 B 场阴影图。

图 9：使用 (a) SV 和 (b) Hys 模型计算的在 t = 75 ms 时的 B 场箭头图。

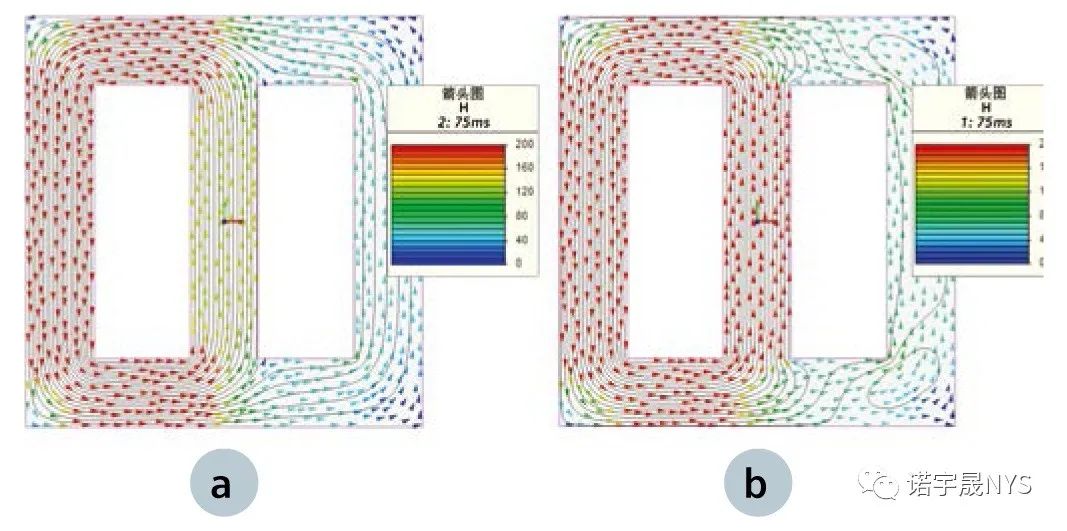
图 10：使用 (a) SV 和 (b) Hys 模型计算的在 t = 75 ms 时的 H 场箭头图。

使用两种材料模型的两个线圈的电压和磁链分别如图 11(a)和 (b) 所示。由于 B 场和 H 场之间的相位滞后，Hys 情况下的相位差是显而易见的。P 点处线圈电流和磁通密度的计算结果与测量结果分别如图 12 (a) 和 (b) 所示。由于初始磁化曲线，开始的 1/4 激励周期的结果未显示。使用 Hys 模型实现了很好的一致性，这是其用于电磁仿真的一个很好的例子。

11：(a) 两个线圈上的电压，(b) 两个线圈中的磁链，使用 SV 和 Hys 模型。

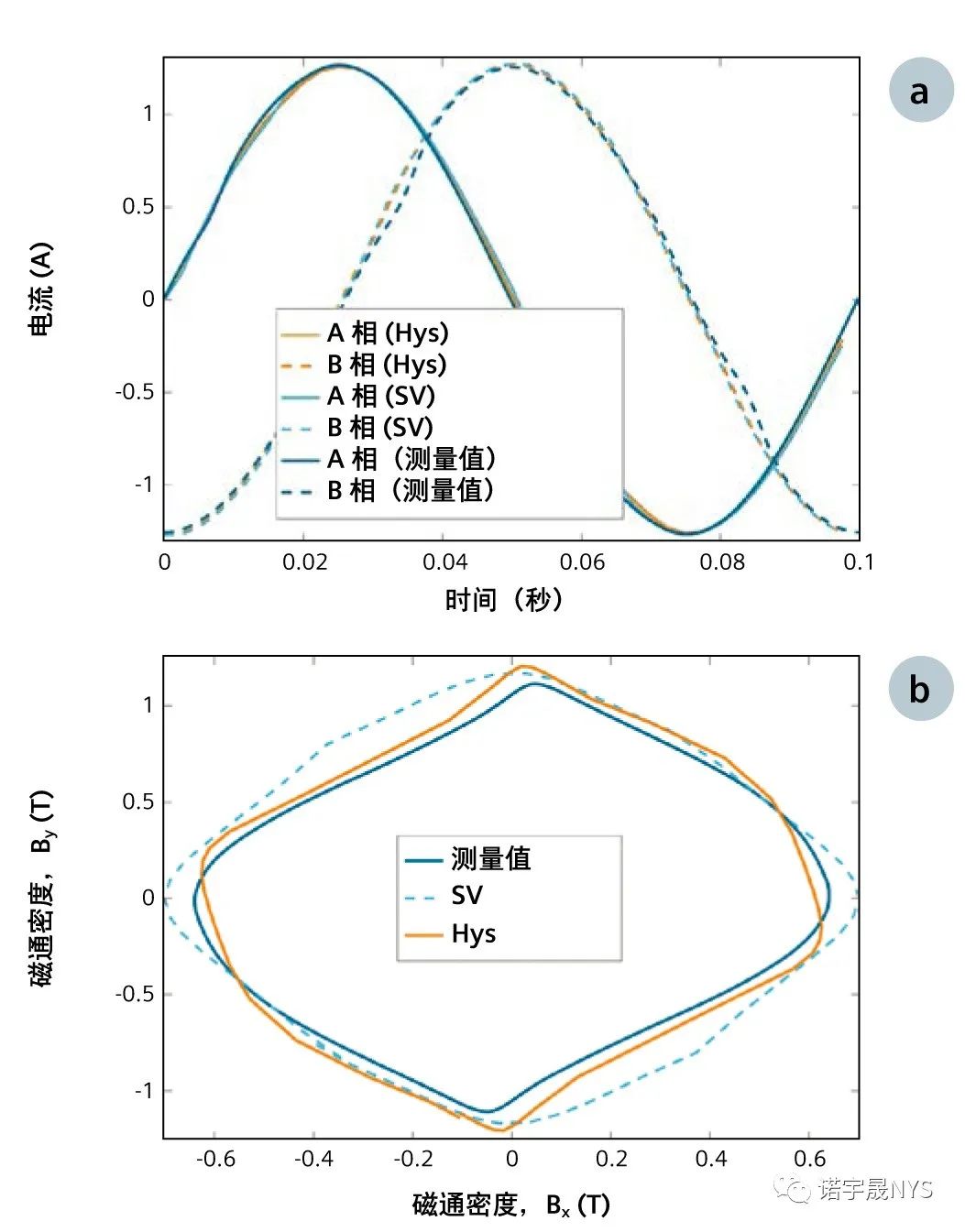
图 12：计算和测量的 (a) 线圈电流，以及 (b) P 点处的 Bx 和 By 通量密度。

3.执行器

在该实例中，负载驱动的电磁执行器使用 Transient 2D 和 Simcenter MAGNET 中的运动求解器来仿真。执行器的仿真模型如图 13 (a) 所示。执行器中的线圈由充电至12V 的电容器驱动。弹簧将柱塞抵在上止挡处。在时间t = 0 时，开关闭合，充电电容器连接到线圈。本体和柱塞均采用 M47 – 24 Ga 钢制造。

对于 SV 和 Hys 模型，在 t = 26.9 ms 时计算的 B 场的阴影图分别如图 13 (a) 和 (b) 所示。这里没有太明显的区别。然而，我们希望精确预测柱塞在任意时间的位置。图 14 (a) 显示了使用两种模型计算的位置（作为时间的函数）之间的差异，可以观察到 SV 和 Hys 情况之间的滞后。这对于需要知道精确位置的关键应用非常重要。使用两种模型计算的线圈电流也显示在图 14 (b) 中。

图 13：(a) 执行器的 Simcenter MAGNET 模型。使用 (b) SV 和 (c) Hys 模型计算的在 t = 26.9 ms 时的 B 场阴影图和箭头图。

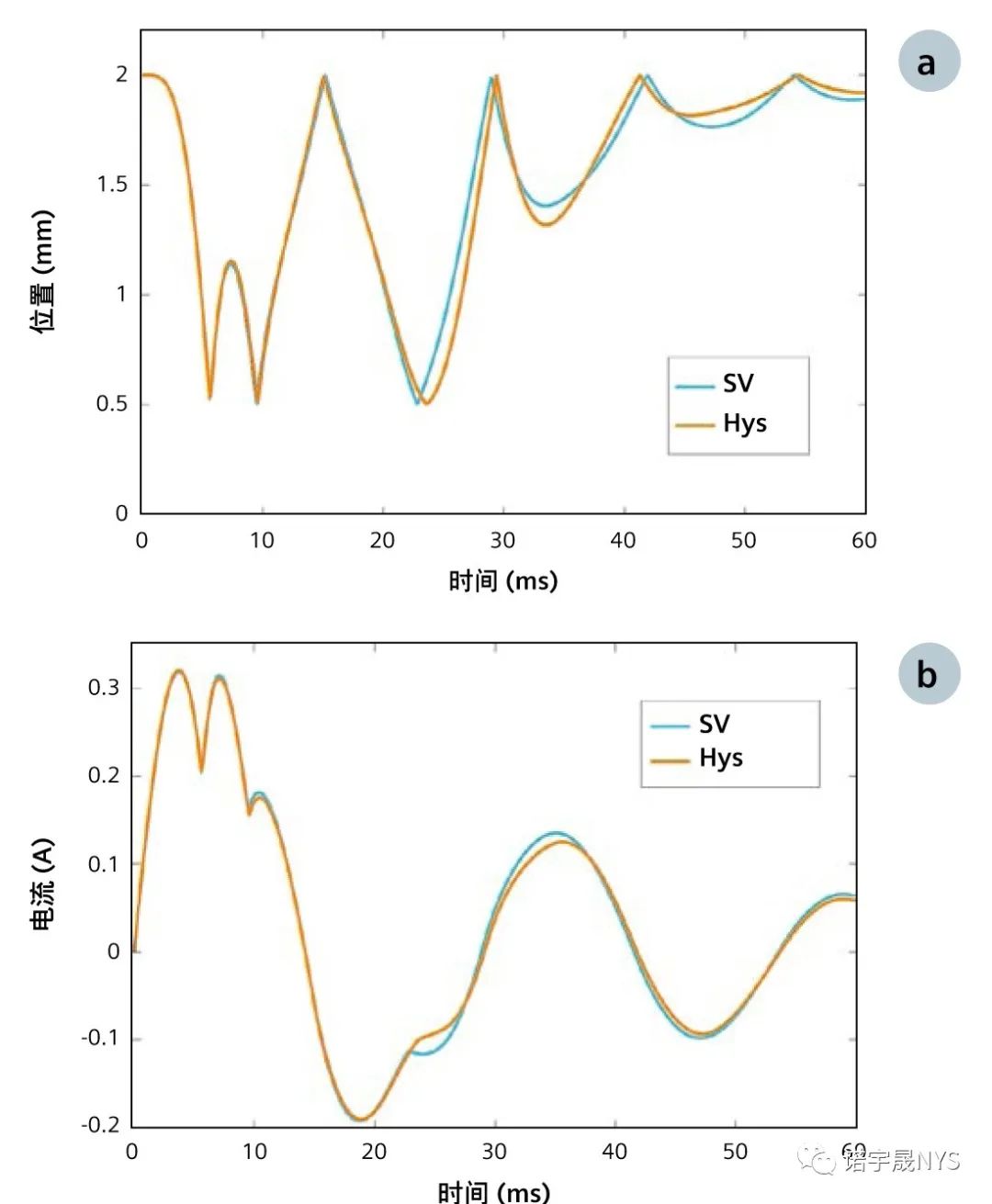
图 14：使用 SV 和 Hys 模型计算的 (a) 执行器的位置和 (b) 励磁线圈电流。

4.感应电机 

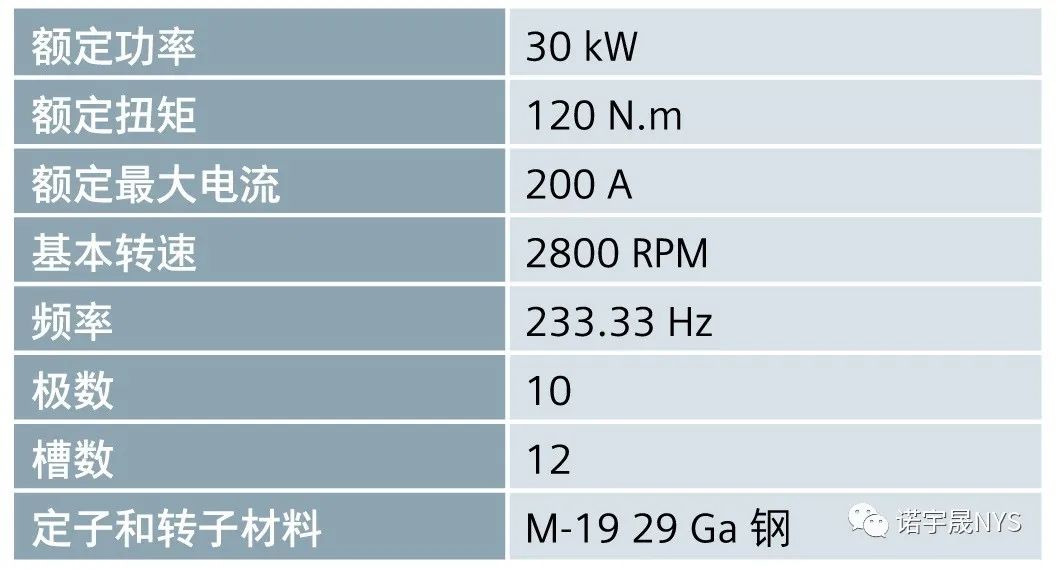
这里介绍电压驱动感应电机的 Simcenter MAGNET 仿真。测试电机的额定规格如表 2 所示。

非斜槽电机的完整 Simcenter MAGNET 模型如图 15 所示。出于仿真目的，使用四分之一模型，采用二维运动瞬态求解器求解了 25 个供电周期（频率 = 50Hz）。对于SV 和 Hys 模型，图 16 显示了 t = 500ms 时计算得到的B 场的阴影图。可以看到，两种模型在 500ms 时的的转子位置有差异。

表 2 – 感应电机规格

图 15：36 槽、28 导条、4 极感应电机的 Simcenter MAGNET 模型。

图 16：使用 (a) SV 和 (b) Hys 模型计算的在 t = 500 ms 时的 B 场阴影图。

A 相的磁链和电流分别如图 17 (a) 和 (b) 所示。可以看到，求解的结果中存在瞬态。Hys 模型预测电流波形中的过冲较高，但瞬态消失的速度比 SV 模型快，因为铁磁材料中的能量耗散改变了系统的时间常数。这也意味着在这种情况下可以更早地实现稳态，运行磁滞仿真的时步数可以更少。感应电机可被视为一类旋转变压器。因此，在变压器仿真中同样会有类似的结果。

图 17：使用 SV 和 Hys 模型计算的 A 相 (a) 磁链和 (b) 相电流。

感应电机的转速和扭矩特性分别如图 18 (a) 和 (b) 所示，可以观察到类似的瞬态特性。稳态下的值没有明显差异。

图 19 显示了电机各部分的时间平均功率损耗（磁滞损耗、涡流损耗和欧姆损耗）。这里没有给出转子的磁滞损耗，因为滑差频率（本例中为 0.5Hz）非常小，在 Hys 情况下获得转子频率的一个完整周期的时间平均磁滞损耗将需要非常多的求解步。

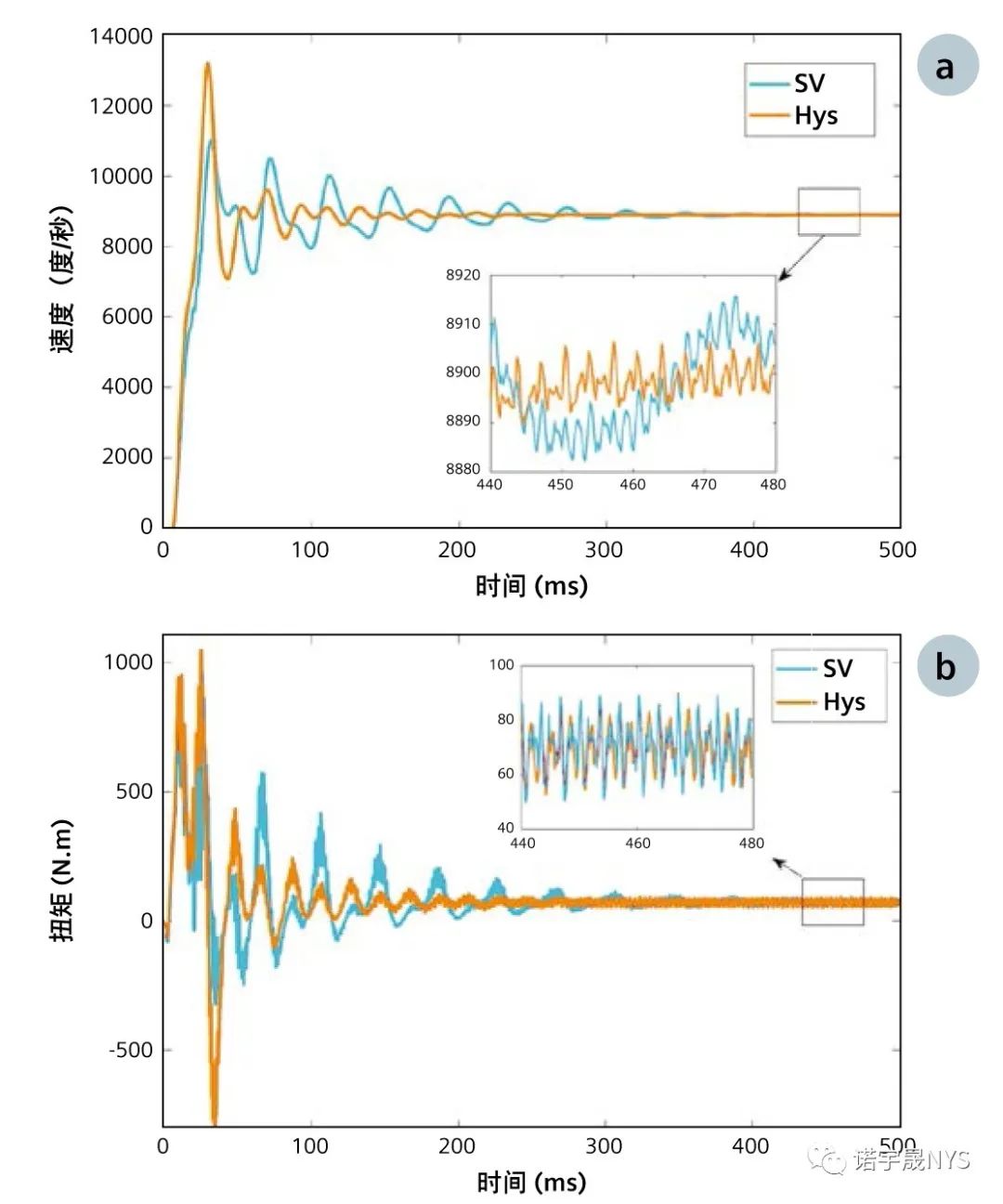
图 18：使用 SV 和 Hys 模型计算的 (a) 转速和 (b) 扭矩。

图 19：使用 SV 和 Hys 模型计算的电机不同部分的功率损耗。

5.表贴式永磁体分数槽内转子电机

本例说明了用于牵引应用的表贴式永磁体 (SMPM) 分数槽、集中绕组、同步电机的电流驱动仿真。电机的规格如表 3 所示。

表 3 – SMPM 电机规格

SMPM 同步电机的完整 Simcenter MAGNET 模型如图 20 所示，使用带运动的二维瞬态求解器在低速（频率 = 50 Hz） 高扭矩区域对五个供电周期进行求解。使用 SV 和 Hys 模型，在 t = 0 ms 时计算的 B 场的阴影图分别如图 21 (a) 和(b)所示。可以看到，SV 情况下定子齿处于深度饱和状态（约 2T），这意味着 SV 磁化曲线的外推高估了场值。

图 20：12 槽 10 极表贴式永磁体分数槽电机的 Simcenter MAGNET 模型。

图 21：使用 (a) SV 和 (b) Hys 模型计算的在 t = 0 ms 时的 B 场阴影图。

使用 SV 和 Hys 模型计算的 A 相的磁链和电压分别如图22 (a) 和 (b) 所示。Hys 情况下的磁链小于 SV 情况；当使用 Hys 模型时，可以看到齿槽效应对电压的影响。使用两种材料模型计算的扭矩如图 23 所示。在使用 Hys 模型的情况下，铁损被包含在场结果中，因此产生的扭矩小于 SV 模型的扭矩。使用两种模型计算的铁损没有很大差异，如图 24 所示。

图 22：使用 SV 和 Hys 模型计算的 A 相 (a) 磁链和 (b) 相电压。

图 23：使用 SV 和 Hys 模型计算的扭矩。

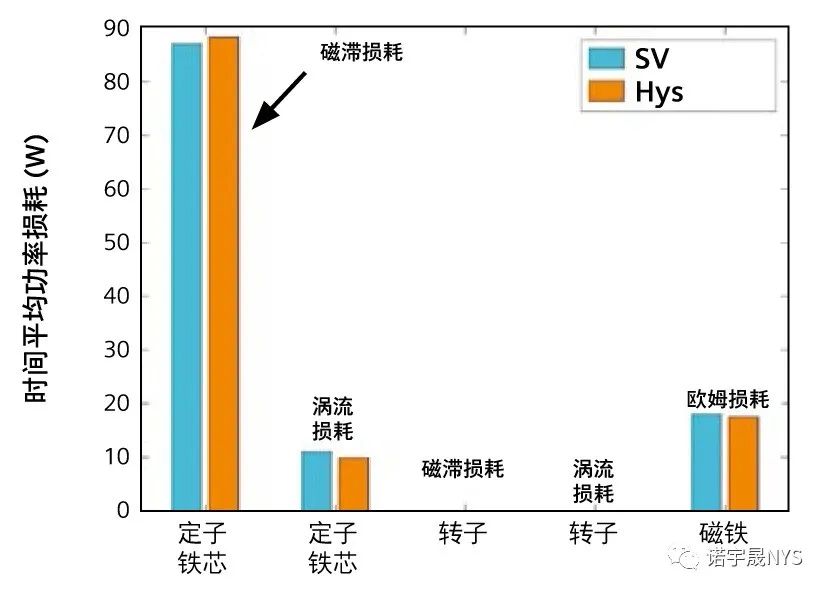
图 24：使用 SV 和 Hys 模型计算的电机不同部分的功率损耗。

Hys 模型的时间性能对用户很重要。对设计工程师而言， 一般并不希望解决方案需要花费太多计算时间。使用 SV 和 Hys 模型求解上述实例的总仿真时间如表 4 所示，其比率如图 25 所示。

需要注意的是，该图对 Hys 模型与 SV 模型的时间性能估计进行了比较，具体时间性能会随着每个周期的时步数、网格密度、多项式阶次等的不同而有很大变化。用于收集表 4 所列数据的求解器设置如下：每个周期的时步数 = 100，多项式阶次 = 2，牛顿容差 = 1%。将牛顿容差降低到非常小的值会增加非线性迭代次数，造成仿真时间显著延长。

表 4 – SV 和 Hys 模型的仿真时间比率

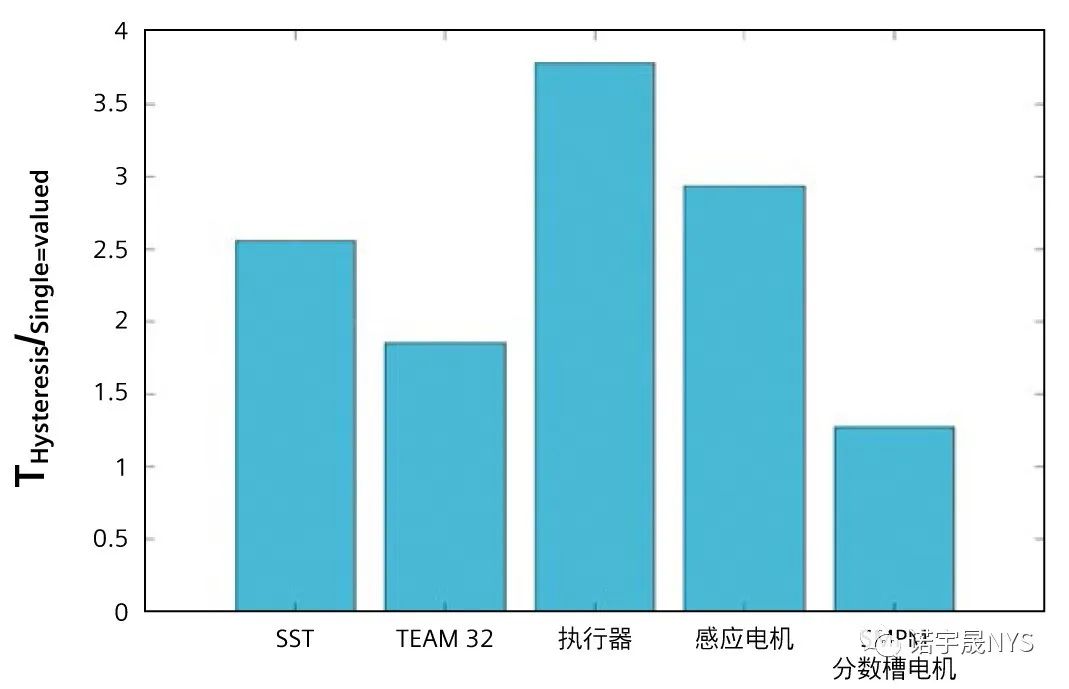
图 25：Hys 模型与 SV 模型的时间性能比较。